受験生数的処理、いざ勉強すると全然解けないんだけど
公務員試験の数的処理が初見で解けない！と悩む人は非常に多いです
大丈夫！それが普通です！
そして実は数的処理は正しく対策すれば、誰でも大きな得点源に変えることができます
僕自身、数的処理が分からずに悩んでいましたが勉強法を変えたら一気に伸びました
この記事では数的処理が「苦手」から「得意」にかわる具体的な方法を分かりやすく解説していきます
- 数的処理が難しく感じる理由
- 具体的に解き方を例題解説
- 数的処理が得意になる方法
数的処理に拒否反応がある人こそ、ぜひ最後までご覧ください！
ハンター公務員大丈夫やで！解けないって落ち込むなよ！
・工学部卒
・新卒でブラック企業戦士となる
・28歳で公務員試験の受験を決意
・地元の社会人予備校に通う
・80時間の残業をしながら8か月間勉強
⇒県庁、市役所、国税専門官に合格
「公務員になりたい人」のため情報発信中！
>詳細プロフィールはこちらから
数的処理が初見でできなくても問題なし！難しく感じる理由3つを解説
受験生初見で解けなくてもいいの？
ハンター公務員全然問題ないよ！それが普通やから安心して！
数的処理を初見で解けないからといって、今焦る必要はまったくありません
ここではなぜ初見の数的処理は難しく感じるのかを解説します
難しく感じる理由を知れば、焦りやいら立ちが消えて「今やるべき対策」に集中することができます
学校では習わないから
数的処理は「論理的に考えてパターンに当てはめる」という解法が必要な科目です
計算問題をゴリゴリ解く、学校の数学とは全く異なります
そのため、これまで勉強したことのない問題が多く、初見で解けなくて当たり前です
実際、僕は工学部出身で理系だったのに数的処理はめちゃくちゃ苦労しました
ハンター公務員え？全然分からんやん！ってなったわ
逆に言えば、数学ができる、できないはほぼ関係ありません
今から正しい勉強をしていけば誰にも伸ばすチャンスがありますよ！
安心して進んでいきましょう！
パターンを覚えるのが大前提の科目だから
数的処理は解法パターンを覚えていることが前提の科目なので、初見で解けないのは当然です
難しいと感じる原因は、その場でゼロから解法を考えようとすることにあります
そうではなく数的処理を得点源に変えるには、次の進め方が鉄則です
解法を理解する→覚える→解法に当てはめて解く
このように解法を正しく理解してパターン化できれば、問題に対してのアプローチが一気にシンプルになります
そして、数をこなすほどどんどん精度とスピードが上がっていきます
受験生たしかに何度かやっていると、またこのパターンか！ってなるね！
ハンター公務員そうやろ？それがどんどん蓄積されて得点になるで
今は解答を見ないと手も足もでない人もそれで間違っていないので安心してください！
解法パターンが増えていくと、少しずつ伸びていきますよ
出題範囲が膨大だから
数的処理と一言でいっても、出題範囲はかなり広いです
これらを全部やろうとした結果、挫折してしまう人が非常に多いです
まんべんなく対策するのは大間違いなので、やめましょう
数的処理は優先度を決めて対策すれば、一気に楽になる
実際、僕自身は講師に出題頻度の高い分野だけに絞ってもらうことで、得点が急に安定しました
落ち着いて優先度を決めて取り組めば、あなたも数的処理が得点源に変わっていきます
焦らず、正しい順番で積み上げていきましょう
ハンター公務員毎年どんな問題がどれくらい出てるかとか正味分からんやろ？
僕もこの部分は講師に頼んだよ
僕のように数的処理が苦手でどうにもならなくて不安な人は、通信講座も選択肢に入れると気持ちがラクになります
まず下記の記事で通信講座の全体像をサクッと確認だけしてみてくださいね
数的処理はどんな科目？特徴を解説
数的処理は、公務員試験における最重要科目です
ハンター公務員苦手やからやらんは通用せん
不可避の科目やで。
数的処理の特徴
誰でも得点源にできる可能性がある一方で、配点が高いため苦手なまま放置すると非常に危険です
受験生重要なのはわかったけど…
ひとりは不安だし失敗しそうや…
そう感じた人はあなたに合う通信講座がないか、簡単に確認してみてくださいね
出題分野は数的推理・判断推理・資料解釈に分けることができる
数的処理は3つの分野に大別できます
それぞれの出題範囲は以下のとおりです
数的推理の出題範囲
- 速さ
- 旅人算
- 流水算
- 通過算
- 割合
- 比
- 売買算
- 濃度
- 順序・組み合わせ
- 確率
- 倍数・約数
- N進法・数列・規則性
- 方程式
- 仕事算・ニュートン算
- 平均算・年齢算
判断推理の出題範囲
- 論理命題
- 集合
- 対応関係
- 位置関係
- 順序関係
- 勝敗関係
- 嘘つき
- 暗号
- 推理
- 多角形と角度
- 三角形と長さ・面積
- 三平方の定理
- 円・扇形
- 相似
- 立体図形
- 軌跡・折り紙
- 積み木・投影図・立体断面
- 展開図・多面体
- 一筆書き
資料解釈の出題範囲
- 実数の表
- 構成比の表
- 増加率の表
受験生おいおい。こんなに広いとか無理ゲーじゃない？
これだけの範囲があっても、しっかり優先順位をつけて対策すれば得点源に変わります
時間が足りない人や、初めて数的に挑む人は、通信講座も一度確認しておきましょう
ハンター公務員僕も思い切って講師に頼んでめっちゃのびたで！
独学でがんばりたい人は最適な参考書・問題集を選びましょう
下記の記事で、数的処理の参考書20冊を実際に買ってレビューしてみました
ぜひ参考書選びの参考にしてください！
論理的思考能力が試される
数的処理は3つの分野で求められる能力が少しずつ異なっています
- 数的推理
条件や文章、図表などの情報から、数学的な知識を使って論理的に考えて正しい答えを導き出す問題
- 判断推理
条件や文章、図表などの情報から、論理的に推論して正しい答えを導く問題
- 資料解釈
資料やグラフを読んで正しく情報を理解する能力
その中で、共通して必要な能力が論理的思考能力です
どんな問題も自分の中で正しくロジックを立てて、問題を読み進めていく必要があります
自治体は論理的に考えられる人かを知りたい
僕は公務員として実際に働いたから分かりますが、公務員の仕事はロジックでガチガチに固められています
その根幹になる論理的思考能力を試すために数的処理があることを理解しておいてください
ハンター公務員だからこんなに配点が高いんやで！
どんな試験でも配点が高い超重要科目！得意に変わると一気に得点源になる
| 数的推理 | 判断推理 | 資料解釈 | 教養試験に占める数的処理の割合 | |
|---|---|---|---|---|
| 国家一般 | 3 | 8 | 3 | 47% (14/30) |
| 国家総合 | 3 | 8 | 3 | 47% (14/30) |
| 地方上級全国 | 7 | 9 | 1 | 34% (17/50) |
| 市役所等 | 4 | 8 | 2 | 35% (14/40) |
| 裁判所一般 | 4 | 10 | 1 | 50% (15/30) |
| 特別区 | 5 | 10 | 4 | 40% (19/48) |
| 東京都 | 5 | 7 | 4 | 40% (16/40) |
受験生めちゃくちゃ出題されてるやん！
ハンター公務員そう。だからすごく大切な科目やで
数的処理はどんな試験でも出題数が非常に多く、教養問題の3～5割を占めているのが最大の特徴です
ここを落とすと、他で挽回するのはかなり厳しいです
- 苦手で面白くないから…
- 専門試験で挽回すれば良いんでしょ
こんな考えがいかに危険かが分かってもらえたかと思います
僕自身も独学しているときは「嫌いだから後でやる。」と思っていましたが、甘かったです
ハンター公務員予備校で講師から喝！をもらったで
僕の場合は勉強の優先順位を見直してもらって、数的処理を第一に勉強するようにしました
結果、数的処理が得点源となり試験を突破することができました
同じように「間違った選択をしたくない人」は、講師のサポートを検討してみてください
>通信講座の比較をサクッと1分チェック！
あなたも数的処理が得点源になれば、筆記試験突破が大きく近づきますよ
【実体験】苦手な人がとるべき対策はこれ！数的処理を得意に変える対策3選
受験生もうすでに苦手意識でいっぱいなんだよ
センスがなくて拒否反応が出そうだよ
ハンター公務員センスとかは関係ないよ！
取り組み方教えるわ
ここでは僕自身が、数的処理を得意に変えた実体験からとるべき対策を解説していきます
解法を「理解」して覚える
大切なのは「解法のパターン」を徹底的に覚え込むことです
今は自分で解けなくて良いので、解答を読み込んで解き方を理解して覚えてください
注意点は、解答だけを丸暗記するのはNGということです
そこに至るまでの「解法を理解」してストーリーで記憶しましょう！
ハンター公務員流れで覚えたら暗記の量も減ったよ！
また、公務員試験は時間との勝負です
毎回、その場で解き方を考えていたら絶対に時間が足りないので注意しましょう
ハンター公務員僕は解法パターンに当てはまらん！って判断したらその問題は捨ててたで
頻出分野に集中して勉強する
数的処理は膨大な範囲の中から出題されます
出題範囲はこちらを参照
結論、まんべんなく勉強はダメです
理由はシンプルで、本番で点につながるのは「頻出分野」だからです
受験生でもどこに集中して対策したらいいの？
ハンター公務員独学の人は自分で決めなあかんな
講座取ってる人は講師に従おう
試験種や年度によって、頻出分野や配点バランスは普通に変わります。
まず勉強する前に、自分が狙っている自治体の情報収集からスタートしましょう。
- 自分で判断するのは不安…
- 遠回りはしたくない
そう感じた人は、数的処理に強い通信講座の全体像だけ一度確認してみてください。
ハンター公務員高額な講座は一切不要やで！
解法がわからない問題はすぐに聞いて解消する
受験生解答を見ても分からんところがあるんだけど
数的処理の勉強を進めていくと、必ず分からない問題にぶつかります
ここで大切なのは「分からない」を残さないことです
僕が独学していた時は誰にも聞けず、分からないことはそのまま丸暗記して覚えていました
しかし、いざ他の問題を解いてみると全然解けませんでした
- どのパターンがいいか分からない
- 1mmも手が動かない
- また解答をみて暗記量だけが増えていく
ハンター公務員原因は解説を論理的に理解できてなかったからやな
数的処理は丸暗記だけでは歯が立たない
講師に質問できる環境を手に入れてからは、明らかな変化がありました
- 別の問題が同じ問題に見える
- 暗記の量が減る
- 解くスピードが上がる
ハンター公務員解法への理解が進んで明らかに伸びたで。
数的処理は「分からない」を積み重ねることが、致命傷になります
分からないことはすぐに聞いて解消しましょう
受験生手軽に聞ける環境がないよ…
という人は、まず質問制度のある通信講座を確認してみましょう。
優良な通信講座を比較した記事を置いておくので、参考にしてみてください
>通信講座の比較をサクッと1分チェック！
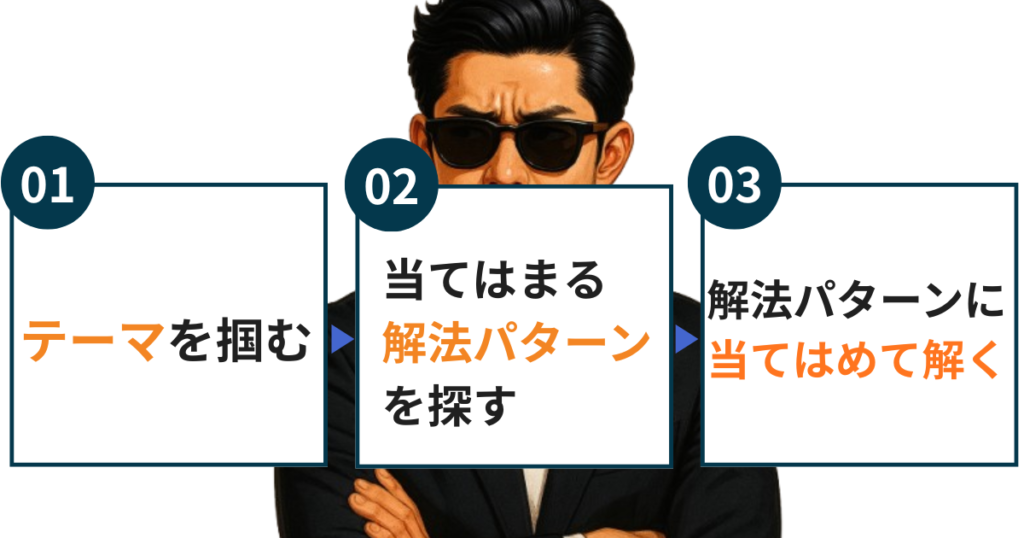
数的処理の具体的な解き方とコツを3ステップで解説
ハンターとAさんが1から30までを交互に数えていく
最後に30と言った人が負けとなる
1回につき最大3つまで数えることができて、必ず1つは数えないといけない
先行のハンターが勝つためには、一回目にいくつ数えれば良いか答えよ
-選択肢-
- 1つ数える
- 2つ数える
- 3つ数える
受験生具体的にどんな感じで解いたらええの？
ハンター公務員上の例題で3ステップ解説するで
問題文をサッと確認してテーマを把握する
受験生じゃあさっそく計算していくで
ハンター公務員これダメ！！
まずは問題をサッと読んで、問題のテーマを把握しましょう
例題の場合は、「必勝法」のジャンルだとぱっと分かります
どの解法パターンに当てはまるかを考える
テーマが分かったら、自分が覚えた解法パターンでどれが使えるかを考えます
必勝法の問題は必ず勝つための条件を見つけ出すことがポイントです
ここを全力で探しましょう
例題の場合は、30を言ってしまうと負け→つまり29を言って相手に回答権を渡せば絶対にハンターは負けません
つまりハンターが29を言えるように逆算していきます
ここがこの問題の最大のポイントです！
解法パターンに当てはめて解く
ここまできたら、あとは解くだけでOKです
例題の場合、相手の回答と自分の回答の合計をコントロールできないか考えます
お互い1、2、３のいくらかを数えるので、相手がどれを言ってもハンターの回答次第で合計4に操作することができます
ということは4×7=28となり7回目のやり取りで28になることが分かります
つまり先攻のハンターは最初に1を数えておけば、29を確実に言うことができます
よって答えは1回目に1を言っておけば負けない
厳密に言えば、1回目に1を数えたあとは相手と自分の数字の合計が4になるように足し算していけば負けないということです
ハンター公務員今は分からなくてOKよ！
この問題で一番大切なのは29を言うってことやな
数的処理がどうしても苦手なあなたへ
ここまで読んで
- やっぱり数的処理だけは苦手かもしれない
- ひとりで勉強しても解けるようになる気がしない
そう感じている人もいると思います。
- 出題範囲が広い
- 思考の型が分からないと手が止まる
- 分からないまま進むと一気に詰む
という、独学ではつまずきやすい科目だからです。
ハンター公務員僕自身がどうにもならん！ってなったから、痛いほどわかる。
そういう人は、「講師に頼る選択肢」があることを知っておいてください。
- 数的処理が苦手で困っている人
- 費用をおさえて対策したい人
- 頻出問題だけに注力したい人
- 分からないことをすぐに質問したい人
いきなり高額な講座を選ぶ必要はまったくありません。
まずは、数的処理に強い通信講座がどんな内容なのかを確認することからスタートしましょう。
先にネタバレすると、僕は公務員のライトの数的処理フルパックをおすすめします
実際に買って受講してみた結果、おすすめできると判断しました！
気になった人だけ、下記の記事で解説しているので確認してみてください
＼ハンター公務員からの申し込みで最大3,000円OFF／
数的処理に関するよくある質問
数学が苦手ですが、数的処理に影響しますか？
数学の得意・不得意は数的処理には影響しません
数学的な知識よりも、論理的に考える力が必要な科目だからです
誰でも勉強すれば得点源にできる一方で、数学が得意でもしっかりと対策しないと得点できません
ハンター公務員数的処理に特化した勉強が必要やで！
数的処理は捨て科目にしても良いですか？
数的処理は一日どれくらいの時間をかけて対策すればいいですか？
これはどんな勉強をしているかによるので一概に言えません
参考に僕の場合を紹介します
- 独学のとき・・・適当でした(0～3時間くらい)
- 予備校のとき・・・講師に決めてもらった問題をやったら終わり(1時間くらい)
ハンター公務員講師にやるべきこと決めてもらったら楽だったね
独学の人は自分で決めるしかない！
どの分野から勉強すればいいか分かりません
これは正解がありません
ハンター公務員最終的に合格できたらそれが正解やからな
ただし、合格ノウハウをもつ講師から教えてもらっている人は考えなくていい部分です
そのまま問題を解くことだけに集中しましょう
独学の人は、お使いの参考書の中で頻出とされている問題に取り組みましょう
数的処理でおすすめの参考書はありますか？
数的本が圧倒的におすすめです
詳しくは下記の記事で徹底解説しています。
独学で数的処理を勉強するのは難しいですか？
はい。厳しいです
独学が厳しい理由は下記の記事で解説しています
そしてあなたは数的処理だけを対策すればいいわけではないですよね？
他の教養科目や専門科目も同時に対策していかなくてはいけません。
効率よく数的処理をものにするためには、まずは手軽に受講できる通信講座を確認してみてください。
>通信講座の比較をサクッと1分チェック！
数的処理が初見で解けないのは当然！正しく対策して得点源に変えよう！
受験生数的処理が初見で解けないんだ
ハンター公務員大丈夫！不安にならんでいい！
数的処理が初見で解けないのは当然なので落ち込む必要はありません
必ず他の受験生もぶち当たる壁だからです
ですがそのまま放置するか、正しく対策するかで結果は大きく変わります
数的処理は次の3つを意識するだけで、少しずつ「解ける問題」が増えていきます
- 解法の型を知る
- 頻出分野に集中する
- 分からない所を放置しない
どうしてもひとりでは不安！という人は、講師に頼るという選択肢があることも覚えておいてください
>通信講座の比較をサクッと1分チェック！
ハンター公務員僕自身、講師に頼んでめっちゃ伸びたから検討してみてね！
この記事があなたの数的処理の得点を1点でも底上げできることを祈っています
ではでは！
